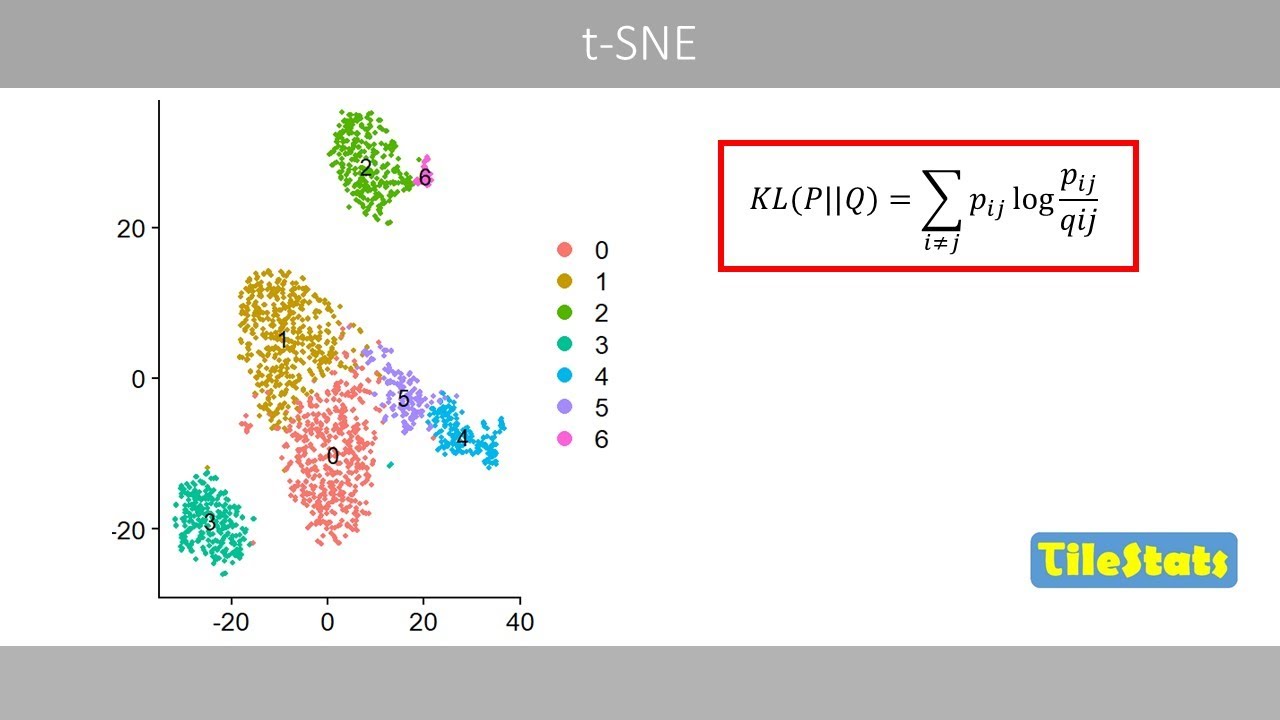
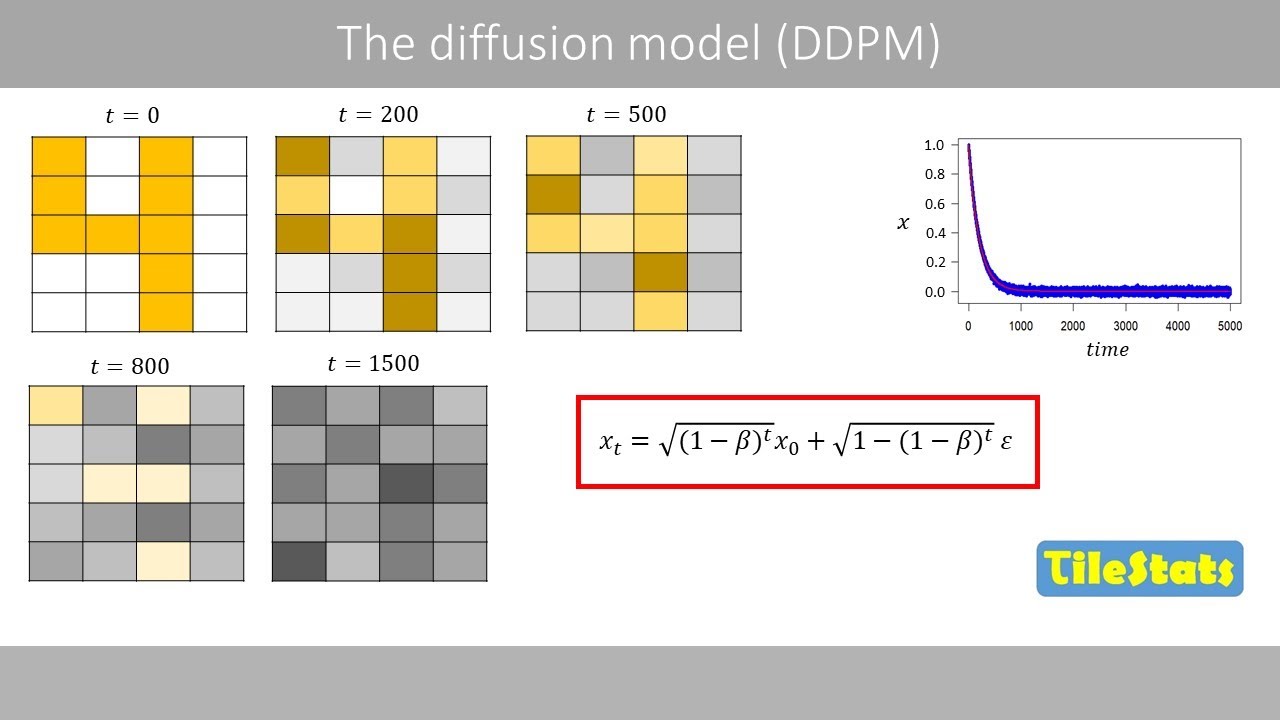
UMAP explained simply
Now Playing
UMAP explained simply
Transcript
438 segments
We will here have a look at UMAP which
is a similar method to the TE method
that I covered in a previous video. UAP
stands for uniform manifold
approximation and projection which is a
dimension reduction method that captures
both local and global structures of
highdimensional data. The UMAP method
was published in 2018.
I will first show some applications
where UMAP can be used and compare it
with principal component analysis. Then
we will have a look at the simple
example that explains the basic math
behind UMAP. We'll first see how UMAP
and PCA perform on a classical amnes
data set which contains thousands of
images of handwritten digits. Every row
in this data set contains pixel values
between 0ero and 255 for each image. The
first column shows which digit the image
contains. For example, the first row
represents an image of a handwritten
five whereas the second row represents
an image of a handwritten zero and so
forth. Each image is a square that
contains 784 pixels, which means that
each image or row has 784 columns in
addition to the first column. Suppose
that we like to generate an image of the
data that is located on row number six.
We would then put the elements in column
numbers 2 to 29 here. Then the next 28
elements here, and so forth.
until we have a square matrix with 28
rows and columns. This image is supposed
to represent a handwritten two. We'll
now use UMAP and PCA to compress these
784 columns into just two columns and
plot these columns in a two-dimensional
plot.
We will then label the points in the
plot so that we can see which point that
corresponds to a certain digit. Similar
to PCA, UMAP is an unsupervised method
because it does not use these labels in
its computation to separate groups or
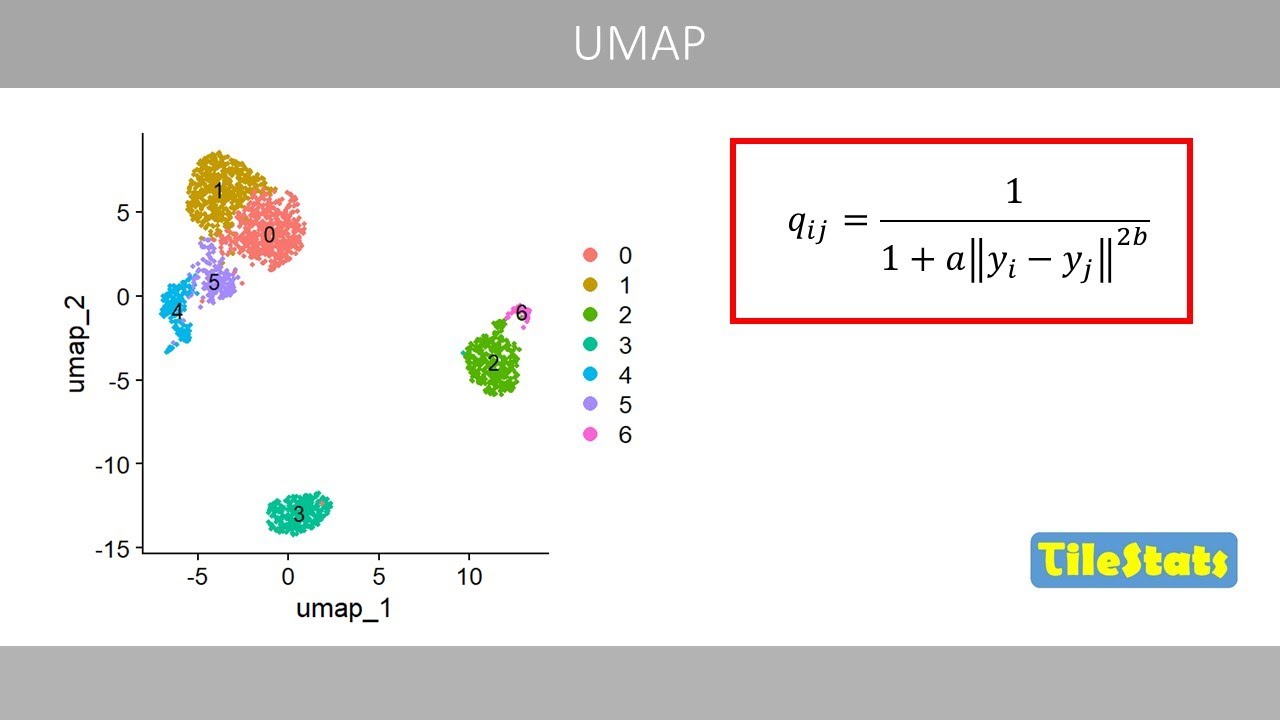
clusters. This is an example of a UMAP
plot of 10,000 images in the MNEST data
set. Each point in this image represents
one image. For example, this point
represents the following handwritten
eight
whereas this point represents a four. We
can see that the UMAP separates the
images of the 10 digits quite well. In
comparison, this is the corresponding
PCA plot of the MNEST data set which
fails to separate the digits. I will
explain why in a minute. Um plots are
commonly used in single cell RNA
sequencing to visualize highdimensional
gene expression data in two dimensions
to identify clusters of cells with
similar expressed genes. Each point in
this um plot represents a single cell.
Points in the same cluster can be seen
as cells that have a similar gene
expression profile. Such a cluster of
cells therefore usually represent cells
of the same cell type. For example, the
clusters may represent different cells
in our immune system. If you were to use
PCA on the same data set, the clusters
would not separate well. So why is this
the case? Well, one reason is that a PCA
plot usually only shows the first two
principal components because these
explain most of the variance. By
illustrating only the first two
components, which in this case only
explain about 5% of the total variance,
we lose a lot of information that is
stored in the other components.
For example, we can see that cluster two
and six are not well separated based on
the first two principal components. If
you instead plot component one versus
component five, clusters two and six are
now well separated. The um method does
not hold important information in
several components like this. Instead,
it includes all information in just two
dimensions, which explains why the UMAP
plot better identifies clusters that
exist in the highdimensional data.
However, the UMAP method is
computationally expensive, which is why
it is sometimes combined with PCA. One
can therefore compress the variables by
first using PCA and selecting for
example the first 30 to 50 components
that store most information and then
computing the UMAP based on these
components instead of all variables.
Another reason why PCA might fail to
separate existing clusters is that it is
a linear method. For example, if we were
to project this nonlinear
two-dimensional data set into one
dimension, the clusters will not
separate well with PCA.
Whereas the UMAP would do a good job in
separating the existing clusters because
it preserves local nonlinear
relationships.
Although these points are fairly close
in the global geometry, UMAP tries to
preserve also the local structure.
Close points are assigned a high
connectivity weight indicating a strong
likelihood of being neighbors which
means that also these points have a high
connectivity weight and so forth.
A UMAP is controlled by these two
hyperparameters
that are set by the user. The parameter
ns can be seen as the number of
neighbors each data point selects for
its local neighborhood in the
highdimensional space. The effect of
this parameter is shown on the amnest
data set. A small value focuses more on
local structures which might fragment
some clusters.
A larger value focuses the plot more on
the global structure where clusters may
overlap a lot. The default value of 15
is usually a good value to use that
captures both local and global
structures.
The parameter mean distance controls the
minimum distance between points in the
lowdimensional space that I will explain
later on. A low value results in tight
clusters
whereas a two high value might cause
overlapping clusters.
Setting these two parameters to 15 and
0.2 gives a nice um plot based on the
amnes data set.
The parameter spread was not described
in the original UMAP paper but has been
included in several implementations to
control the distance between the
clusters. Increasing the value of this
parameter increases the distance between
the clusters in the MNEST data set. We
will now discuss the basic math behind
UMAP.
The math that I will show comes mainly
from appendix C in the paper where they
explain U mapap in a similar way to the
tney method which is a lot simpler to
understand.
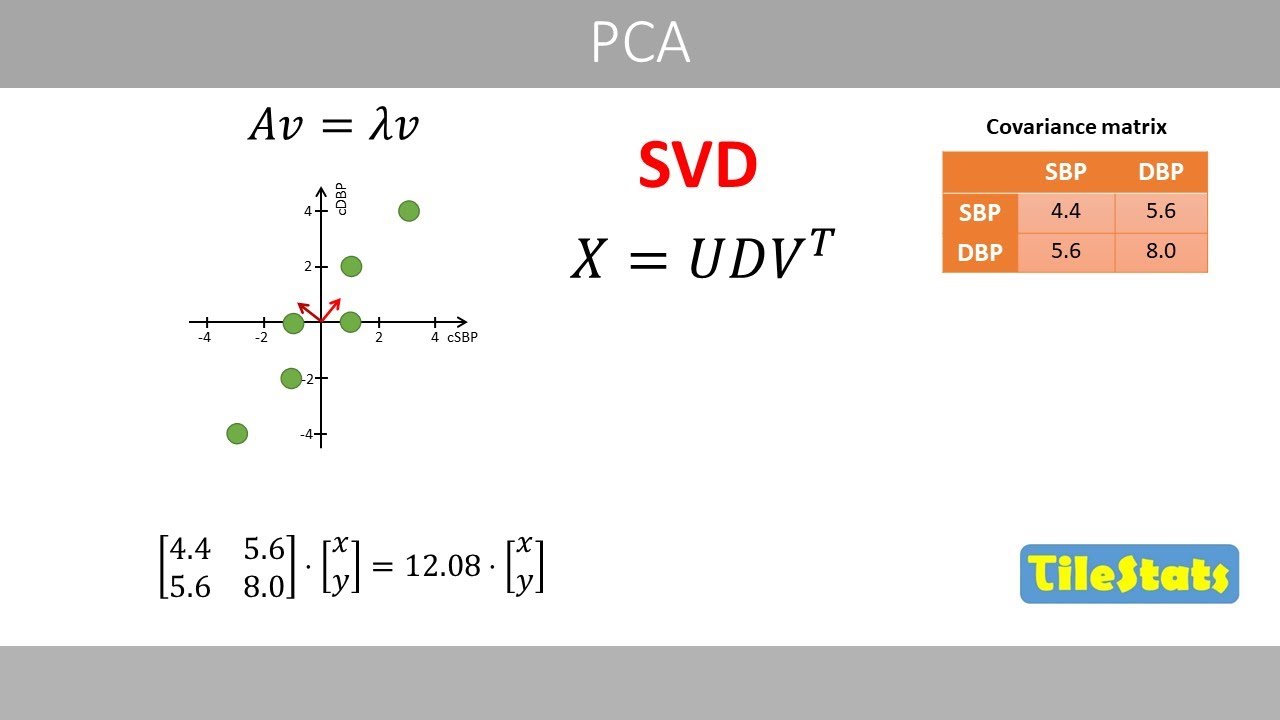
We will use a similar three-dimensional
data set as in the video about Tney and
use the same random initial coordinates
in two dimensions.
UMAP may either use initial random data
points like this or points initialized
based on the method of spectral
embedding.
We'll here see how UMAP reduces the
dimensions of this highdimensional data
into lowdimensional data. In other
words, how it reduces three-dimensional
data into two-dimensional data. In
comparison to Tesney, which uses a
Gaussian like distribution that I
explained in the Tesney video, um uses
an exponential kernel based on some
distance metric. I will here use the
Cleian distance. Um uses this equation
to compute a symmetric matrix whereas
Tney uses this equation. UMAP starts by
calculating for example the client
distances between all data points of the
original data in the highdimensional
space.
For example, if we were to calculate the
client distance between data points one
and five. We will plug in the X, Y and Z
coordinates in this equation
and do the math. We now plug in the
rounded ecclesian distance in a distance
matrix.
If you calculate the distances between
all data points in our data set, we
would get the following values. For
example, we can see that the ecclesian
distance between data points two and
four is 5.19.
Let's put the cleon distances based on
the highdimensional data set here.
Next, we determine the value of K, also
called N neighbors. The default value is
usually 15, but since we have a small
data set, we set this value to three.
This means that when we consider, for
example, the distances between data
point one and all the other four data
points, we only focus on the three
closest points to data point number one.
For example, these are the three closest
neighbors to data point number two. And
these are the three closest neighbors to
data point number three. And so forth.
For data point one, we plug in its
shortest distance here, which is its
distance to data point number three. And
then we plug in the distance between
data point one and two. Here we set
sigma to one for now and do the math.
Then we plug in the distance between
data points one and three. We skip this
distance because data point 4 is not one
of the three closest points to data
point one. Finally, we plug in the
distance between data points one and
five.
If you do the math in the numerator,
we will get these values. This is an
exponential distribution where sigma
determines the area under the curve.
Since sigma is set to one, the area
under the curve is now one. If you plug
in the calculated values in the
numerators in the exponential
distribution,
we can see that the heights of the curve
correspond to these values.
Sigma is now optimized
so that the sum of the heights
is equal to the log base 2 of the
hyperparameter ns.
Remember that we previously set the
hyperparameter n neighbors to three.
Sigma is now adjusted
so that the sum of the heights
is equal to 1.58.
If you set sigma to 0.648,
the sum will be equal to about 1.58.
Note that the area below the curve is
now 0.648.
Since the area below the car must be
equal to one to be defined as a
probability distribution, the
unnormalized exponential function used
in UMAP is instead referred to as an
exponential kernel. This is the adjusted
VIGs for different optimized values of
sigma for each row. Note that every row
now sum ups to about 1.58.
These dots represent the distances that
we did not consider because they were
not among the three closest neighbors.
This is therefore a sparse matrix. A
sparse matrix is more computationally
efficient to work with because the
memory use is n * k instead of n * n.
These elements, including data points
that are not the three closest
neighbors, are set to zero.
Next, we symmetriize this matrix by this
equation where the symmetric distance
value between for example data points 2
and 4 is equal to 0.2993.
If you do the same calculations for the
other values, we will get these values.
Note that the upper triangle
holds the same values as in the lower
triangle, which means that we have a
symmetric matrix.
These are the normalized distances for
the highdimensional data that will be
compared with the distances of the
lowdimensional data. Next, we compute
the distances for the lowdimensional
data with this equation. This equation
has two parameters that are optimized
based on the hyperparameter mean
distance that is set by the user. I will
explain how these values are calculated
at the end of this video. If you set the
hyperparameter mean distance to 0.5.
A will be equal to 0.576
and B will be equal to 1.363.
If a and b are set to one, we'll get the
same expression as in the numerator of
the corresponding equation for the tnne
method. We start by calculating the
cleian distance between the points in
the low dimensional space. These are our
initial random coordinates in two
dimensions.
To calculate the cleon distance between,
for example, data point one and three in
the low dimensional space, we plug in
the x and y coordinates and do the math
and plug in the resulting value in the
distance matrix. If you calculate the
distances between all data points, we
will get this matrix.
We can now plug in the client distances
in this equation and compute the first Q
value like this which we plug in into
the Q matrix.
If we compute the other values, we'll
get the following Q matrix in which the
main diagonal is set to zero. These
values will be adjusted by comparing
them
with the values in our previous
symmetric V matrix based on
highdimensional data by using the
following cross entropy cost function
that we minimize with the gradient
descent method.
We here only need to include the values
in the upper triangles.
If we compute the value of the cost
function based on the upper triangles,
we get a value of about 7.7.
We'll now change the coordinates of the
points in the lowdimensional data
and update the values in the Q matrix
to reduce the value of the cost
function. UAP uses stochastic gradient
descent to do this. But to simplify the
calculations, I've here just used the
gradient descent method.
To compute the gradient descent, we need
to find the derivative of this function,
which looks like this. We know the
values of A and B and the values in the
V and Q matrices and the coordinates of
the points in the low dimensional data
and the corresponding ukian distances.
We'll here see how to calculate the
derivative based on the first data
point.
We plug in these values
here
and then these values
here.
Then we plug in the clear distances
between data point one and all the other
data points
here.
Next, we plug in the x and y coordinates
of data point one and the coordinates of
the other data points
and do the math.
Note that this calculation is based on
more exact numbers of the values in the
Q matrix and the distance matrix.
If you do the calculations for all rows,
we'll get these values
which we plug in into the gradient
descent formula
where alpha is the learning rate that we
here set to 0.01.
These are our current coordinates in the
low dimensional space.
So if we multiply these values by the
learning rate and subtract the resulting
values from these values,
we'll get these updated values.
And the coordinates of the data points
will therefore be updated like this.
Note that data points four and five have
now moved closer to each other so that
the location of the points in the low
dimensional space are similar to the
ones we see in the high dimensional
space.
With these updated values, we have
reduced the cost function from 7.7 to
6.9.
If we repeat the same calculations 200
times, we'll get the following plot
which closely resembles what we see in
the highdimensional space.
After 200 iterations, these are the
values in the Q matrix which closely
match those in this matrix.
Finally, I will explain how the
parameter mean distance is related to
the parameters A and B. The red curve is
the target curve that takes the exact
shape based on the parameter mean
distance. The mean distance controls the
length of the flat part of this curve.
If the distance is shorter than or equal
to the mean distance parameter, the
value of the curve is equal to one. And
if the distance is longer, the curve
follows an exponential decay function.
Now we use nonlinear regression to fit
this function to the points on the
target curve for a range of different
distances
so that we get the following fitted
curve where a and b are estimated to the
following values. If you will plug in
these values here and change the value
of d between zero and six we would get
this blue curve. So when we plug in the
distances in this function, it can be
seen as we compute the heights of this
fitted curve based on the distances
between for example data point one and
the other data points.
If you increase the mean distance from
for example 0.5 to one, the flat part of
the fitted curve increases and the
distances between the data points
increase so that we get about the same
optimal Q values.
The points are therefore forced to keep
more distance between them when we
increase the parameter mean distance.
This explains why the data points are
more spread out within the clusters when
we increase the parameter mean distance.
This was the end of this video about
UMAP. Thanks for watching.
Interactive Summary
Ask follow-up questions or revisit key timestamps.
This video explains UMAP (Uniform Manifold Approximation and Projection), a dimension reduction technique that captures both local and global structures of high-dimensional data. It compares UMAP with Principal Component Analysis (PCA), demonstrating UMAP's superior performance in separating clusters in datasets like handwritten digits (MNIST) and single-cell RNA sequencing data. The explanation delves into the mathematical underpinnings of UMAP, including how it constructs a high-dimensional graph using an exponential kernel and then optimizes a low-dimensional representation using cross-entropy. Key hyperparameters like 'n neighbors' and 'min distance' are discussed, along with their impact on the resulting visualizations. The video also touches upon how UMAP can be combined with PCA for computational efficiency and explains the role of the 'spread' parameter.
Suggested questions
3 ready-made promptsRecently Distilled
Videos recently processed by our community