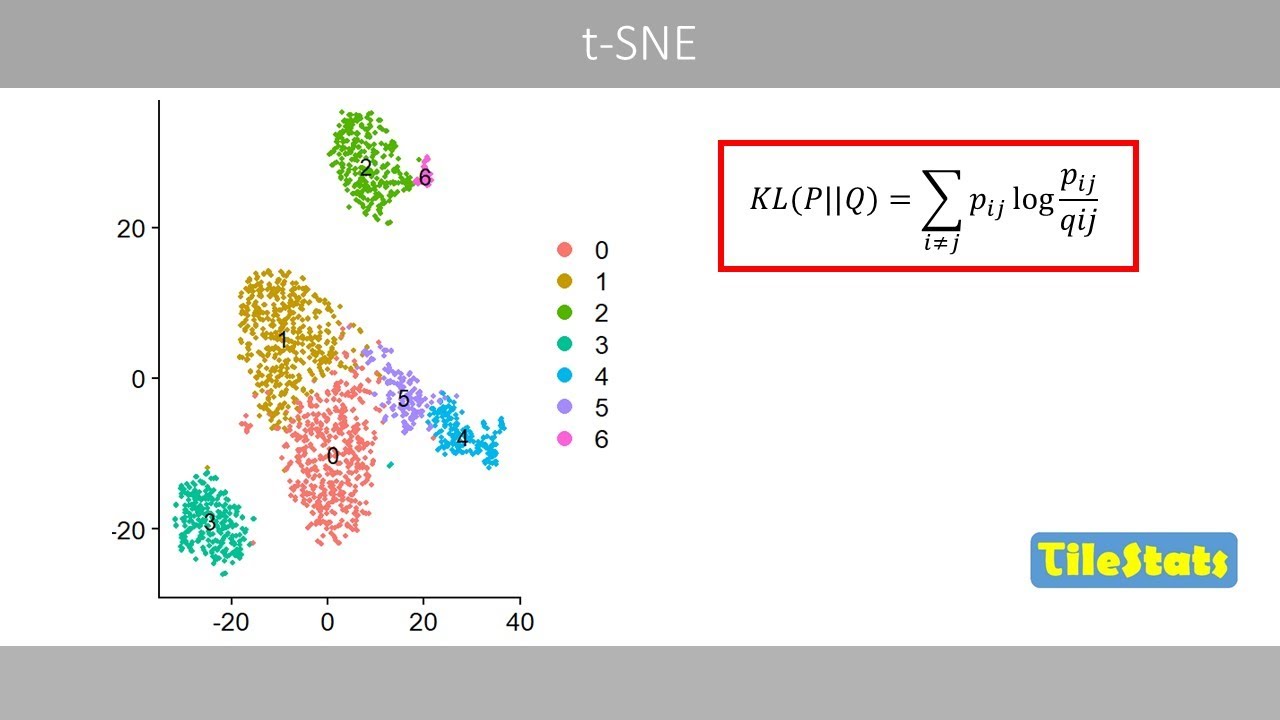
PCA and SVD - the math explained simply
Now Playing
PCA and SVD - the math explained simply
Transcript
570 segments
In this video, we'll talk about the
mathematical details behind the
principal component analysis. I will
here assume that you have some basic
knowledge about matrix operations and
vectors. If not, check out these videos.
I will first explain the main idea
behind PCA and then show the math step
by step to compute the PCA by the
encomposition method and discuss its
relation to the singular value
decomposition method SVD before we have
a look at how to compute these methods
by using some simple R and Python code.
Finally, I will try to explain why the
EN vectors are useful in PCA.
To explain how PCA works, we will use
the following simple example data. For
example, person number one has a
diastolic blood pressure of 78 and a
systolic blood pressure of 126.
Whereas this data point corresponds to
the blood pressure of person number two
and so forth. So PCA is all about
combining variables so that we can
reduce the dimensions of the data set.
One simple way to combine these two
variables would be to just add them. 126
+ 78 is 204
and so forth. So this would then be our
combined variable that we call blood
pressure. When we add the variables, it
can be seen as we use this equation
where these weights are equal to one.
The idea with PCA is to put different
weights on the variables so that we
maximize the variance of the combined
variable. The reason why we like to
maximize the variance is because we then
keep as much information as possible in
the combined variable. Note that you
will always lose some information when
you combine variables. Since bun can
just use very large weights to increase
the variance, we need some constraint.
PCA uses the following constraint where
the sum of the squared weights is equal
to one. By using this constraint, the
total variance of the original data will
be equal to the total variance of the
principal components that we will
compute later on.
For example, the weights 0.8 and 0.6
will be valid weights when we combine
the two variables because the sum of the
squared values is equal to one. Let's
try to combine the two variables by
using these weights. Note that we here
put more weight on the systolic blood
pressure because this weight is here
larger than the weight we multiply by
the diastolic blood pressure.
By using these weights, the combined
blood pressure for the first person is
147.6
and the combined blood pressure for the
second person is 150.4
and so forth. This is the combined blood
pressure for all six individuals.
The variance of the combined blood
pressure is 11.072.
Let's try many different weights for our
linear combination to see which
combination that results in the maximum
variance of the combined variable. We
know that the weights 0.8 and 0.6 result
in the variance of the combined variable
of 11.07.
If you instead put more weight on the
diastolic blood pressure, we see that
the combined variable has a higher
variance.
But if you put too much weight on the
diastolic blood pressure, the variance
is reduced.
To maximize the variance, we should
therefore use these two weights. But how
do we find such weights?
Well, there are basically two methods to
find the weights that maximize the
variance. We will start to have a look
at the IGEN decomposition method and
then see how the SVD method works. To
compute PCA by using the IGEN
decomposition method, we can perform the
following steps where we first center or
scale our data. Then we calculate the
covariance matrix on our centered or
scaled data. Next we compute the Igen
values and the IGEN vectors of the
covariance matrix. Finally we order the
IGEN vectors and calculate the principal
components.
Usually one starts to center or scale
the data. In this case we will only
center the data. We therefore subtract
the mean systolic blood pressure from
the individual observations.
These are the centered values which tell
how far away the original values are
from the mean. We then do the same
calculations for the diastolic blood
pressure which has a mean of 82.
We can summarize the centered data in
the following table. If you like to
scale or standardize the data, you
simply divide the center data by the
standard deviation of each variable.
When we center the data, it means that
we center the data points around the
origin.
Centering the data points around the
origin will help us later when we will
rotate the data. After we have centered
the data, we have the following values
which can be plotted like this.
Next, we calculate the coariance matrix
based on the center data. If you instead
scale or standardize the data, the
covariance matrix will be equal to the
correlation matrix.
Note that the main diagonal of the
coariance matrix includes the variance
of each variable.
The sample variance of the systolic
blood pressure is calculated like this.
When we calculate the variance of the
centered data, the calculations become a
bit simpler since the mean of the
centered data is always equal to zero.
To calculate the sample variance of the
centered data, we therefore simply sum
the squared centered values and divide
by the sample size minus one.
Then we calculate the variance of the
diastolic blood pressure.
Finally, we calculate the co-variance,
which is a measure of how much the two
variables spread together. The sample
co-variance is calculated by multiplying
the centered values of the two
variables.
For example, we multiply the centered
values for person number one and then
add that to the product of the centered
values for person number two and so
forth. Finally, we divide the sum of the
products by the sample size minus one.
We see that the spread in the diastolic
blood pressure is a bit higher than the
spread in the systolic blood pressure.
The co-variance is somewhere between
these two values.
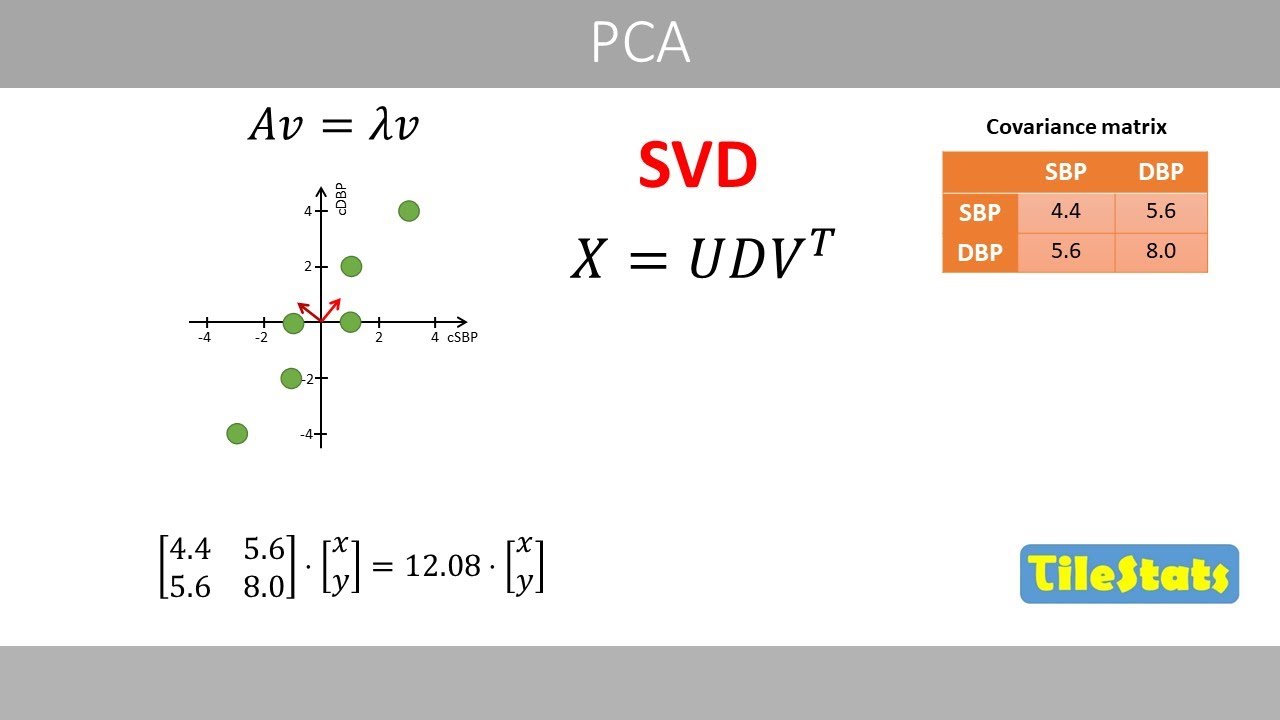
Next, we calculate the igen values of
the covariance matrix.
We substitute a by the co-variance
matrix
and this term by lambda times the
identity matrix which has the same
number of rows and columns as the
covariance matrix.
Subtracting these two matrices results
in the following matrix.
Next we calculate the determinant of
this matrix
which is the product of this diagonal
minus
the product of this diagonal.
After some simplifications
we have the following quadratic
equation. Quadratic equations like this
can be solved in different ways which
will not be discussed here. Anyway, if
you plot how the left hand side changes
as a function of different values of
lambda, we see that the left hand side
is equal to zero when lambda is equal to
either
about 0.32
or 12.08.
These two values represent our values of
the covariance matrix. Next, we
calculate the corresponding vectors to
these two values. We will start by
calculating the igen vector of the
covariance matrix with the corresponding
value 12.08.
To calculate the igen vectors of the
coariance matrix, we use the following
equation that we have discussed in the
previous video about vectors.
We plug in the coariance matrix and one
of the two values. If you multiply the
coarience matrix by this column vector
and multiply the igen value by the same
vector, we'll get the following system
of equations.
We move these two terms to the right
hand side.
After some simplifications, we have the
following system of equations.
Solving for y in the two equations
results in that y is equal to 1.37x.
For example, if you set x equal to 1,
y is equal to 1.37.
This vector is therefore an en vector of
the covariance matrix. We can illustrate
this vector in the plot like this by
drawing an arrow from the origin to the
coordinates
one and 1.37.
We will now normalize this vector to
unit length which means that it should
have a length of one.
The length of this vector is about 1.7.
And if we divide these values by 1.7,
we'll get the igon vector with unit
length.
This vector represents one out of two
vectors of the coariance matrix.
To find the second vector, we do the
same calculations as before based on the
second value. After some calculations,
this vector represents our second vector
with unit length. Since the coariance
matrix is symmetric, its igen vectors
corresponding to distinct values are
orthogonal. Therefore, their angle is
90°.
Next, we order the igen vectors based on
their corresponding igen values where
the igen vector associated with the
largest igen value becomes our first
vector. Since this igen vector is
associated with the largest value, it
will represent our first vector. We
therefore rename this vector so that it
is called v1 instead of v2. Let's put
these two vectors together into a matrix
that we called V. The first column
represents the first vector whereas the
second column represents our second
vector.
We now use this matrix to transform our
center data so that the two variables
are completely uncorrelated.
Let's define our centered data as matrix
X.
Next, we multiply our data matrix X by
matrix V. Then we get a new matrix with
a transformed data. This transformed
data is called principal component
scores or just scores. When we go from
our centered data to the transformed
data, this can be seen as we rotate the
data clockwise until the two en vectors
point in the same direction as the x and
y axis of the plot. The rotated data now
looks like this. Note that the labels of
the axis have now been changed to
principal components one and two.
Let's call the two columns of the
transformed data PC1 and PC2.
If we were to plot this data, we would
get the following plot.
Let's compare the centered data with the
transformed data.
The variance of the systolic blood
pressure is 4.4
whereas the variance of the diastolic
blood pressure is eight.
This is the covariance matrix of the
data. We see that the co-variance is 5.6
which tells us that there is a positive
correlation between the two variables.
When we transform the data, the first
variable called PC1 has a variance of
12.08
whereas PC2 has only a variance of 0.32.
This means that almost all variance is
kept in the first principal component.
If you divide the variance of the first
principal component
by the total variance, we see that the
first principal component captures 97.4%
of the total variance.
Note that the variances of the principal
components correspond to the two values
we calculated earlier. The igen values
of the covariance matrix therefore
represent the variances of the principal
components.
When we study the covariance matrix of
our transform data, we see that the
co-variance between PC1 and PC2 is equal
to zero. Which means that PC1 and PC2
are completely uncorrelated.
Note that the total variance of PC1 and
PC2 is about 12.4 four which corresponds
to the total variance of the original
variables.
Remember that when we multiplied our
centered data by the matrix that
includes the vectors as columns, we got
the transformed data. This is the same
as using the following equation to
calculate the principal components that
we saw at the beginning of this video
where the weights for the first
principal component comes from the first
vector whereas the weights for the
second principal component come from the
second vector. For example, if we would
calculate the corresponding score for
person number six, we would multiply the
centered blood pressure values of person
number six by the corresponding weights.
By adding these products, we would get a
principal component score of five.
Note that the general aim of using PCA
is to reduce the dimensionality of the
data. In other words, we like to reduce
the number of variables we have. But so
far, we have not reduced the number of
variables since we have the same number
of principal components as the number of
variables we started with. Since the
first principal component captures
almost all variance which can be
interpreted as it stores almost all
information about the two variables. We
can simply delete the second principal
component because it includes almost no
information.
As we have seen previously by using the
following equation we can combine the
two variables into just one variable in
a way that maximizes the variance of the
linear combination
we have. so far used the iggon de
composition of the coarience matrix to
compute the PCA. We'll now have a look
at how to compute the principal
component scores by instead using the
singular value de composition.
The SVD method does not involve the
computation of the covariance matrix.
Instead, SVD solves the following
equation which involves numerical
methods so that the product of these
three matrices is as similar as possible
to the data matrix X which is our
centered values.
Solving this equation is generally more
accurate than the igen decomposition
method because it works directly on the
data matrix X without computing the
covariance matrix that may cause
rounding errors. I will not go into all
the details of SVD. Instead, I will try
to explain what this equation means. We
will start by calculating the so-called
grand matrix where we multiply the
transpose of the center data by the
center data which results in the
following matrix.
Note that by multiplying for example the
second column of the center data by the
first row of its transpose
it's exactly the same calculation that
we do in the numerator when we calculate
the covariance between the two
variables.
This means that we will get the
corresponding coariance matrix if we
divide the gram matrix by n minus one.
We'll now compute the igen values of the
grand matrix
which results in the following values.
If we would divide these values by n
minus one, we'll get the exact same
values as when we compute these based on
the covariance matrix. If you now
compute the igen vector based on the
first value,
we will end up with the same vector with
the unit length as we computed based on
the covariance matrix.
So when we compute the igen vectors and
the igen values of the gram matrix
instead of the covariance matrix we get
the same vectors but different values.
We can now create an igen value matrix
of these two values
like this.
Note that when the igen vectors are
multiplied by the igen value matrix and
then multiplied by the transpose of the
igen vectors,
we get the gram matrix.
If you take the square root of these
values,
we will get the so-cal singular values.
The main idea with the SVD method in PCA
is to factoriize a matrix
into three parts
where the rows in their transpose of V,
the vectors tell us how to rotate the
coordinate axis to point in the
directions of maximum variance.
Matrix D tell us how the data stretch
along each of these new axis. Whereas
matrix U tell us where each observation
lies after the rotation before
multiplying by D which may either
stretch or compress the data points
along the new axis. But how do we
calculate matrix U?
Well, the SVD method computes this
numerically. But let's try to do this by
hand. If you multiply both sides by a
matrix V,
this product will result in the identity
matrix because the igen vector matrix is
orthonormal. Next, we multiply both
sides by the inverse of the matrix D
where this product also results in the
identity matrix.
So we now know how to calculate matrix
U.
This is the inverse of matrix D. So if
you multiply matrix X our center data by
the igen vector matrix V and then by the
inverse of matrix D we will get matrix
U.
So this is our certain data. The rows of
the transposed
vector matrix tell us how the data will
be rotated.
Whereas matrix U gives the coordinates
of the data points in their rotated
principal component space before they
are stretched by the singular values in
D. Note that when we multiply these two
matrices,
the xcoordinates of the data points in
the new space are multiplied by 7.77
whereas the ycoordinates of the points
are multiplied by 1.26.
So that this data is stretched out like
this.
So if you multiply matrix U
by matrix D,
we get the final principal component
scores. And if you multiply these by the
transpose of the igen vector matrix,
we will recreate the original center
data points, which is exactly what this
equation tells us.
To compute the final principal component
scores, we may either multiply matrix U
by matrix D
or simply multiply matrix X by the
vector matrix V.
So this is how you would compute the
decomposition in R.
We first create a matrix of our two
variables.
Then we center the data with the
function scale.
If you instead like to scale your data,
you should set this argument to true.
Then we compute the covariance matrix
and the igen vectors of the covariance
matrix. Finally, we multiply the center
data by the igen vector matrix to get
the principal component scores.
We can also use the SVD method by using
the SVD function that will give us the
D, U, and B matrices.
If you multiply the centered data by the
EN vector matrix, we'll get the
principal component scores which are
identical to these scores.
Depending on your data, you might see
some small differences between the
scores of the two methods.
Note that the prome function in R uses
the SVD method and not the en
decomposition.
The corresponding code for computing the
IGEN decomposition in Python can be
written like this.
Note that we here need to sort the igen
vectors so that the first vector is the
one associated with the largest value.
Also note that Python has negative
values for the first vector
which explains why the scores have
opposite signs compared to the example
in this video. To perform PCA with the
SVD method, we can for example use the
PCA class from the skyit learn.
Before we end this lecture, let's try to
understand why the first vector points
in the direction that has maximal
variance.
From our previous calculations, we know
that the first principal component has a
variance of 12.08.
We got these principal component scores
by multiplying the first vector by the
centered values.
So we can define it like this where the
variance of matrix X times the first
vector is 12.08.
From the previous calculations, we know
that the igen value that we computed
based on the covariance matrix is also
12.08.
The variance of the first principal
component is actually equal to the first
value. This is the definition of an igon
vector
where matrix A in PCA is our covariance
matrix which is usually denoted with
this symbol. If you solve this equation
for the value, we will obtain this
equation given that vector V has unit
length. If you plug in the right hand
side here,
we will get this equation.
We want to find a vector V with unit
length that maximizes the variance. If
the length of the vector is equal to
one, the transpose of the vector times
the vector itself should be equal to one
that I showed at the beginning of this
video. When we have a constraint like
this, one method is to use the lrange
multiplier where this term enforces the
values of the vector to fulfill these
conditions.
If we take the derivative of this
equation with respect to v1, we will
obtain the following equation. We now
set the left hand side to zero
because the derivative is equal to zero
when we reach the maximum of this
function.
We can now rearrange this equation and
cancel the twos.
So that we end up with this equation
which is identical to the equation for
the definition of an vector. So this
explains why the first igen vector
points in the direction with maximal
variance. This was the end of this video
about the fundamental math behind PCA.
Thanks for watching.
Interactive Summary
Ask follow-up questions or revisit key timestamps.
This video explains the mathematical details behind Principal Component Analysis (PCA). It covers the main idea of PCA, which is to reduce data dimensionality by combining variables while maximizing variance. The explanation is step-by-step, detailing the Eigen decomposition method, including data centering, covariance matrix calculation, Eigen value and Eigen vector computation, and finally, the calculation of principal components. The video also discusses the relationship between PCA and Singular Value Decomposition (SVD), and provides examples of how to compute PCA using R and Python code. Finally, it clarifies why Eigen vectors are crucial in PCA by showing they point in the direction of maximal variance.
Suggested questions
5 ready-made promptsRecently Distilled
Videos recently processed by our community